Why a 4:1 TUR is Not Enough: The Importance of Analyzing the Probability of False Accept Risk
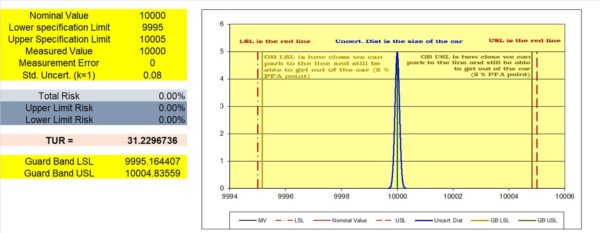
Figure 1 Graph Showing Method 5 Acceptance Limits
Several organizations and publications reference the use of a 4:1 Test Uncertainty Ratio (TUR). Some standards even reference a TUR requirement greater than or equal to 4:1.
The question to ask is if they know why they may need a 4:1 TUR and if they may understand the rationale for requiring a 4:1. The thought here is that a 4:1 ratio is based on specific false accept and false reject risk, and a 4:1 ratio is a simple way of achieving it if certain conditions can be met.
That thought process alone is dangerous if one does not have enough historical data to use a joint probability density function associated with many TUR-based methods.
If one does the math, a 4:1 TUR with a coverage probability of k = 2 for the measurement uncertainty and a 95 % End of Period reliability can equate to less than 1 % false accept and slightly over 1.5 % false reject (these terms are covered later).
In simplistic terms, End of Period Reliability is defined as the number of calibrations resulting in acceptance criteria being met divided by the total number of calibrations. The formula to determine the required sample size from "In-Tolerance" Reliability from historical data is easy to replicate in Excel. The formula is Sample Size = ln(1-Confidence)/ln(Target Reliability)
If we use the formula for Sample Size above, we would need over 59 (58.4) samples to use a joint probability distribution associated with many TUR-based methods.
4:1 may sound good on paper, though many laboratories might use the boilerplate language on a purchase order asking for a 4:1 TUR, likely without the appropriate sample size.
And then, there are different disciplines that, like equipment, cannot easily be grouped into the calculation based on a global risk approach, equipment that might have different usages, fixturing, wear patterns, lots with sub-par quality control, different calibration intervals, and more. These different usages and conditions can lead to statistical independence from the population of like instruments.
When dealing with physical changes to the instrumentation, like material deformation, as found in many force and torque measuring equipment, it isn't the same as if we were measuring the voltage of batteries from a large production lot.
Thus, we must understand the limitations when we analyze requiring a 4:1 TUR as a risk mitigation strategy to control our probability of false accept risk.
Many labs may use a 4:1 TUR properly and understand what decision rule is best to use to manage their application's false accept and reject risks.
The article makes several assumptions relating to standards, assuming the end-user might be requesting a 4:1 TUR based on insufficient sample size. These assumptions are based on the author's perception of what might be happening in the industry.
Measurement Risk
We can think about the risk this way. We have a car and need to park it between two lines. The lines represent the upper and lower specification limit of our device. The width of our car is the uncertainty, and parking lines are our tolerance specification limits.
The probability of us getting a ding or denting another vehicle is our PFA, depending on how centered we are within the parking lines. If we try to park too close to one side, we may risk not being able to open the door, or if we misjudge entirely, we may run right into the car in the other lane and cause substantial damage.
If we park centered on the line, 50% of our car will be in the next lane no matter what size our car is.
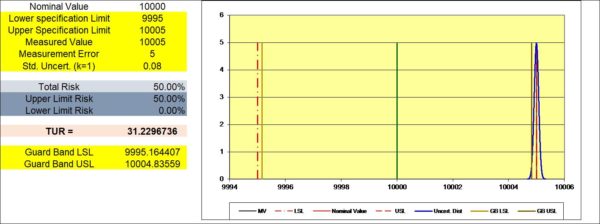
Figure 2 50 % PFA at the Upper Specification Limit
TUR (Test Uncertainty Ratio)
TUR or Test Uncertainty Ratio, defined in Section 3.11 of ANSI/NCSL Z540.3 as “The ratio of the span of the tolerance of a measurement quantity subject to calibration, to twice the 95% expanded uncertainty of the measurement process used for calibration." The TUR helps us control our false reject and false accept risk. [1]
Based on simplicity, the 4:1 TUR seems to be a fallback position many organizations may have adopted and likely continue to use.
NCSLI RP-18 in section 3.5.2 A Critique of the 4:1 Requirement, discusses some Z540.3 TUR requirements that deserve mention. These are:
- The requirement is merely a ratio of UUT tolerance limits relative to the expanded uncertainty of the measurement process. It is, at best, a crude risk control tool, i.e., one that does not control risks to any specified level. Moreover, in some cases, it may be superfluous. For instance, what if all UUT attributes of a given manufacturer/model are in-tolerance prior to test or calibration? In this case, the false accept risk is zero regardless of the TUR.
- The requirement is not applicable when UUT tolerances are single-sided.
- The requirement is only approximately applicable when tolerances are two-sided but asymmetric, and the UUT bias is distributed such that its mode value is zero [2]
In addition, many fail to realize what is described in "Introduction to Statistics in Metrology," section 5.2.1.5 states, "While the 4:1 TUR requirement is commonly used to ensure a measurement is adequate for making an accept/reject determination, this metric assumes that the process distribution is centered between the specification limit. If this is not the case, TUR cannot be reliably used as an indicator of risk" [3]
The reason all of this matters is it is a requirement of ISO/IEC 17025:2017. Section 7.8.6.1 states, "When a statement of conformity to a specification or standard for test or calibration is provided, the laboratory shall document the decision rule employed, taking into account the level of risk (such as false accept and false reject and statistical assumptions) associated with the decision rule employed and apply the decision rule." [4]
PFA Risk
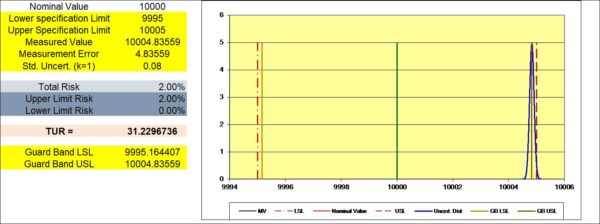
Figure 3 Guard band USL showing a 2 % PFA when Measured Value is at the GB USL.
All measurements have a percentage of likelihood of calling something good when it is bad and something bad when it is good. You might be familiar with the terms consumer’s risk and producer’s risk. Consumer risk refers to the possibility of a problem occurring in a consumer-oriented product; occasionally, a product not meeting quality standards passes undetected through a manufacturer’s quality control system and enters the consumer market.
The Probability of False Accept (PFA) is similar to the consumer’s risk. It is the likelihood of calling a measurement “good” or stating something is “In Tolerance” when there is a percentage that the measurement is “bad” or “Out of Tolerance.” ANSI/NCSLI sub-clause 5.3 is the tolerance-type test requirement that “the probability that incorrect acceptance decisions (false accept) will result from calibration tests shall not exceed 2%.”
With the preponderance of calibrations being of this type, the resources and conditions described by the calibration procedure will require careful evaluation and determination to achieve the measurement uncertainty needed for the calibration process to achieve this allowable probability of false accept.” The measurement uncertainty must be accounted for, and the acceptance limits must be calculated to ensure the likelihood of the measurement being “Out of Tolerance” does not exceed 2%.
Analyzing the PFA is to ensure your measurements are “In Tolerance” with a risk that does not exceed 2%. Just knowing you have a 4:1 TUR without analyzing the PFA regarding the location of the measurement might not be enough to minimize risk, as shown in Figure 3.
Location of the Measurement
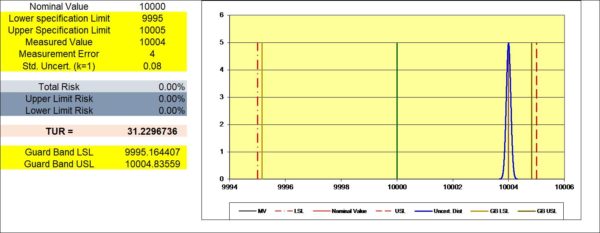
Figure 4 Graph Showing 10,004 as the measured value with a 31.23:1 TUR. is achieved using a lab with low uncertainties.
Calling an instrument “In Tolerance” is all about location, location, location. It's also about the uncertainty of the measurement, but a bad location will raise the Probability of False Accept (PFA) significantly.
The probability of false acceptance is the likelihood of a lab calling a measurement “In Tolerance” when it is not. The location we are referring to is how close the measurement is to the nominal value. If the nominal value is 10,000 lbf and the instrument reads 10,004 lbf, the instrument bias is 4 lbf, as shown in Figure 4.
The larger the bias, the worse the location of the measurement. If we go back to our parking scenario, the worse the bias from nominal, the more likely one side of our automobile will be damaged, or maybe we are still “in tolerance” but have to exit the vehicle from the other side.
Higher TURs help control PFA. If the End of Period Reliability (EOPR) is a fixed value, the TUR will decrease as the measurement process uncertainty increases.
Figure 5 shows this concept as risk level increases as we have switched calibration providers, and the new provider has a higher CMC uncertainty component of 0.025% than shown in Figure 4 where the calibration provider had a 0.0016% CMC uncertainty component; everything else has remained the same.
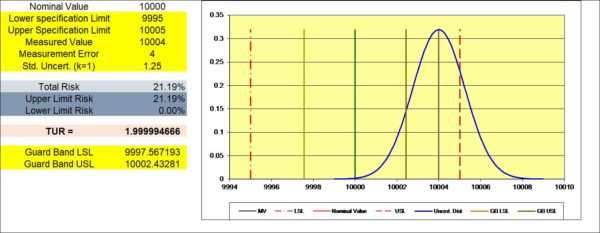
Figure 5 Graph Showing 10,004 as the measured value with a 1.99:1 T.U.R. as the lab's Calibration Process Uncertainty is higher than in Figure 4
Why do we care about the location of the measurement if the device is within tolerance? If a device has a specification of 0.1 % of full scale and the calibrating laboratory reports a value within 0.1%, the device is “In Tolerance,” right?
The answer is and always will be it depends on what the uncertainty of the measurement is and if the lab performing the calibration has adequately calculated their Calibration Process Uncertainty correctly and followed the proper guidelines in determining the uncertainty of measurement when making the statement of compliance.
If the uncertainty of the measurement is significant, the lab performing the calibration will have to be very concerned with the location of the measurement.
If their uncertainty of measurement is too high, they may not even be able to perform the calibration at all, and if the measured value falls right on the specified tolerance line, the PFA can be 50 % or higher.
There are several methods to ensure a 2 % PFA requirement can be met. These TUR-based decision rules typically set acceptance limits to ensure the PFA is less than 2 %.
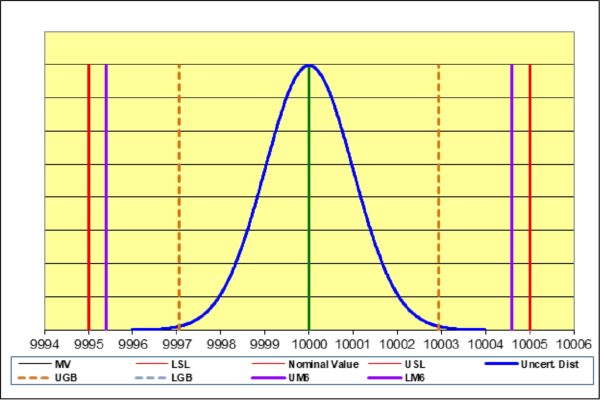
Figure 6 Graph Showing Specification Limits and Acceptance Limits for Both Method 5 and Method 6
Two managed risk guard banding methods to ensure the PFA is less than 2 %
ISO/IEC 17025:2017 section 7.8.6.2 states, “The laboratory shall report on the statement of conformity such that the statement identifies –a) to which results the statement applies; –b) which specifications, standard or parts thereof are met or not met; –c) the decision rule applied (unless it is inherent in the requested specification or standard).”
For this article, we are going to discuss three decision rules. Two of these rules, known as Method 5 and Method 6, are documented in ANSI/NCLI Z540.3 Handbook, and a third rule is something a lab may consider using to meet the criteria.
The standard does not dictate what rules can or cannot be applied. It just requires that the calibration laboratory list the decision rule applied and that the laboratory discusses its decision criteria with the customer.
Guard Band Method 5, Based on the Expanded Calibration Process Uncertainty
This method is simple as one subtracts the 95 % expanded process uncertainty from the tolerance limits. The above graphs in Figures 1 through 4 use Method 5. It is the recommended guard banding method in section 2.3 of ILAC G8:2009 Guidelines on the Reporting of Compliance with Specification.
ILAC G8 states if the specification limit is not breached by the measurement result plus the expanded uncertainty with a 95 % coverage probability, then compliance with the specification can be stated. If one subtracts the expanded calibration process uncertainty from the specified tolerance, the new acceptance limits will assure a PFA of less than 2 %. The only information needed to use Method 5 is the tolerance and the calibration process uncertainty formula in the figure below.

Figure 7 Calibration Process Uncertainty assuming 95% confidence interval
Calibration Process Uncertainty = 2 x the RSS of CMC uncertainty component = Reference labs Calibration and Measurement Capability, Res = Resolution of the test instrument, and Rep = Repeatability of the test instrument.
Note: See ILAC-P14 for more information on how the CMC uncertainty component can be changed.
The downside of Method 5 is that the test limit is based on the worst-case PFA, which means they may be too aggressive (High PFR), resulting in more false rejects from the reference laboratory. Being overly aggressive and needing to adjust more equipment lends one to look for an alternative method.
This method is also simple as it depends only on the measurement uncertainty compared to the specification limits of what is being calibrated. Per ANSI/NCSLI Z540.3 Handbook, “It makes use of an observation that for a given Test Uncertainty Ratio (T.U.R.), there is a maximum PFA value for all values of the M&TE test point in-tolerance probability.
Applying a guard band based on this maximum PFA value and the corresponding TUR ensures that the PFA is 2 % or less, regardless of the in-tolerance probability. It also results in guard bands with acceptance limits that are much larger than that of method 5.
Guard Band Method 6, Based on Test Uncertainty Ratio
This method is also simple as it depends only on the measurement uncertainty compared to the specification limits of what is being calibrated. Per ANSI/NCSLI Z540.3 Handbook, “It makes use of an observation that for a given Test Uncertainty Ratio (TUR), there is a maximum PFA value for all values of the M&TE test point in-tolerance probability.
Applying a guard band based on this maximum PFA value and the corresponding TUR ensures that the PFA is 2 % or less regardless of the in-tolerance probability.” It also results in guard bands with acceptance limits that are much larger than that of method 5.

The downside of Method 6 is it only works with TUR. ratios of 0.76:1 through 4.6:1. Any ratio higher or lower can cause errors by not calculating the acceptance limits properly.
Comparing Method 5 versus Method 6
Below is a table using the same 10,000 lbf device, using the same variables as shown in figures 1-3, which are a 0.01 resolution, and a CMC uncertainty component of 0.0016 % from Morehouse, which was used as the reference laboratory resulting in a 0.08 lbf calibration process uncertainty at the 10,000 lbf pt.
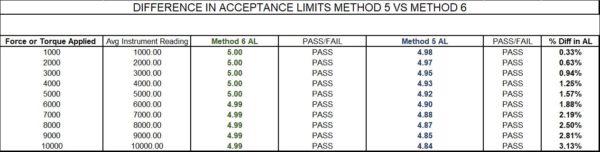
Figure 8 Difference in Acceptance Limits Method 5 versus Method 6 with a CMC Uncertainty Component of 0.0016 %
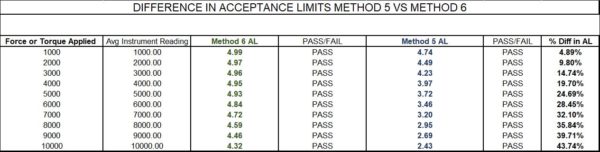
Figure 9 Difference in Acceptance Limits Method 5 versus Method 6 with a CMC Uncertainty Component of 0.025 %
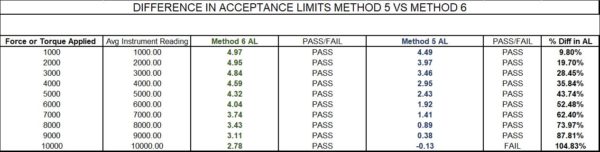
Figure 10 Difference in Acceptance Limits Method 5 versus Method 6 with a CMC Uncertainty Component of 0.05 %
When we analyze the data in Figures 8 through 10, it becomes apparent that the differences between Method 5 and Method 6 become quite drastic as the calibration process uncertainty increases. The CMC uncertainty component of the reference laboratory impacts the calibration process uncertainty, the resolution of the Test Instrument, and possibly the repeatability of the Test Instrument, which may or may not have been included in the calibration process uncertainty.
The laboratory with the low CMC uncertainty component in Figure 8 shows the least amount of % difference from using Method 5. However, the formulas are based on the measurement process uncertainty, which includes the UUT’s resolution and repeatability.
If the resolution and the repeatability of the UUT were to increase, the % difference would increase. Method 5 is the most affected as we subtract the measurement process uncertainty from the specification limits.
Figure 10 shows the calibration laboratory would not be able to use Method 5 under any scenario and make a statement of conformance. However, using Method 6 allows that same laboratory to make a statement of conformance, assuming the measured value falls within the specified tolerance limits.
Conclusion
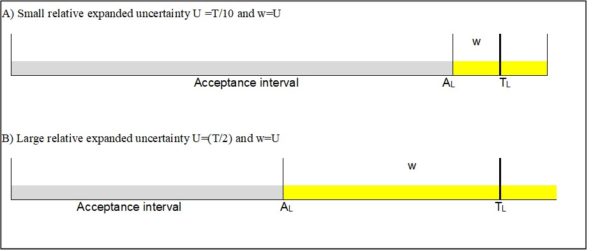
Figure 11 Difference between a large and small calibration process uncertainty
Any method used for calculating PFA will have positives and negatives associated with implementation. The new ISO/IEC 17025:2017 standard does a much better job of addressing measurement risk by requiring the laboratory to report which specifications are not met and the decision rule applied.
The decision rule should use a managed risk guard band to provide a false-accept risk between 1 % and 2 % for most in-tolerance probabilities and TUR.
The author has demonstrated throughout this paper that TUR only shows the ratio of the specified tolerance compared with the calibration process uncertainty. If the ratio is manageable, a laboratory may be able to make a statement of compliance or conformance with either ISO/IEC 17025 standard.
The best chance of continually meeting tolerance requirements assuming EOPR is a fixed value is to use a reference lab (Calibration vendor) with the lowest CMC uncertainty component that replicates how the instrument is used. Also, the end-user must purchase the right equipment capable of continually achieving the desired result or adjust the tolerance appropriately.
More information on the use of proper adapters can be found here.
Want to learn more?
Henry Zumbrun presents webinars and teaches force classes at Morehouse Instrument Company about twice a year, where the participants can learn more about the proper practices to ensure measurements are compliant with the new ISO/IEC 17025:2017 and provide the tools to help minimize force and torque measurement errors. Learn more about upcoming Training opportunities.
To learn more, watch our video on Understanding Test Uncertainty Ratio (TUR).
References
[1] Requirements for the Calibration of Measuring and Test Equipment, 2006, ANSI/NCSL Z540.3-2006
[2] NCSLI RP – 18 Estimation and Evaluation of Measurement Decision Risk
[3]Crowder, Stephen; Delker, Collin; Forrest, Eric; Martin, Nevin. 2020. Introduction to Statistics in Metrology. Springer Nature Switzerland AG.
[4] ISO/IEC 17025:2017 General requirements for the competence of testing and calibration laboratories
[5] Handbook for the ANSI/NCSL Z540.3-2006, 2009, ANSI/NCSL International
[6] ILAC-P14:09/2020 ILAC Policy for Uncertainty in Calibration
If you enjoyed this article, check out our LinkedIn and YouTube channel for more helpful posts and videos.
Everything we do, we believe in changing how people think about force and torque calibration. Morehouse believes in thinking differently about force and torque calibration and equipment. We challenge the "just calibrate it" mentality by educating our customers on what matters and what causes significant errors, and focus on reducing them.
Morehouse makes our products simple to use and user-friendly. Also, we make great force equipment and provide unparalleled calibration services.
Wanna do business with a company that focuses on what matters most? Email us at info@mhforce.com.



