How Do I Calculate TUR?
How to Calculate TUR. Correctly calculating Test Uncertainty Ratio (TUR) is crucial because it is a commonly accepted practice when making a statement of conformity. It helps you analyze measurement risk and is often used in decision rules.
Although TUR is defined in the ANSI/NCSL Z540.3 Handbook and ILAC G8, these universal standards are not always followed. Furthermore, these standards have different formulas for calculating the denominator. To address this frequently misunderstood calculation, we have written this blog to answer, “How do I calculate TUR?”
The TUR Numerator
The numerator of the TUR formula is defined in the ANSI/NCSL Z540.3 Handbook as “the span of the tolerance of a measurement quantity subject to calibration” [1] and in ILAC G8 as "the tolerance, TL, of a measurement quantity" [2]. These definitions are similar, but if the tolerance is not symmetrical, then ANSI/NCSL Z540.3 is much clearer. The TUR formula in the ANSI/NCSL Z540.3 Handbook includes the numerator "Span of the ± UUT Tolerance," which is the difference between the upper specification limit and the lower specification limit for the Unit Under Test (UTT).
The TUR Denominator
There are two different ways to define the TUR denominator. You can use the formula from the ANSI/NCSL Z540.3 Handbook or use the ILAC G8 and ILAC P-14 together to get an almost identical formula.
TUR Formula from the ANSI/NCSL Z540.3 Handbook
TUR is defined in the ANSI/NCSL Z540.3 Handbook as "the ratio of the span of the tolerance of a measurement quantity subject to calibration to twice the 95% expanded uncertainty of the measurement process used for calibration." [3]
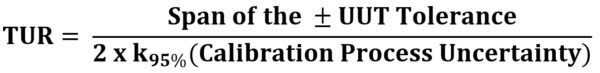
Figure 1: TUR Formula found in the ANSI/NCSL Z540.3 Handbook
The ANSI/NCSL Z540.3 Handbook goes on to explain, "For the denominator, the 95 % expanded uncertainty of the measurement process used for calibration following the calibration procedure is to be used to calculate TUR. The value of this uncertainty estimate should reflect the results that are reasonably expected from the use of the approved procedure to calibrate the M&TE. Therefore, the estimate includes all components of error that influence the calibration measurement results, which would also include the influences of the item being calibrated except for the bias of the M&TE. The calibration process error, therefore, includes temporary and non-correctable influences incurred during the calibration such as repeatability, resolution, error in the measurement source, operator error, error in correction factors, environmental influences, etc." [4]
ILAC G8 and ILAC P14 Definition for the Denominator
In ILAC G8, TUR is defined as "The ratio of the tolerance, TL, of a measurement quantity, divided by the 95% expanded measurement uncertainty of the measurement process where TUR = TL/U." [5]
ILAC P14 further explains what should be included in the denominator, "Contributions to the uncertainty stated on the calibration certificate shall include relevant short-term contributions during calibration and contributions that can reasonably be attributed to the customer's device. Where applicable, the uncertainty shall cover the same contributions to uncertainty that were included in the evaluation of the CMC uncertainty component, except that uncertainty components evaluated for the best existing device shall be replaced with those of the customer's device. Therefore, reported uncertainties tend to be larger than the uncertainty covered by the CMC." [6]
ILAC P14 also addresses when the UUT's resolution and other contributions need to be included in the formula. It states, "When it is possible that the best existing device can have a contribution to the uncertainty from repeatability equal to zero, this value may be used in the Evaluation of the CMC. However, other fixed uncertainties associated with the best existing device shall be included." [7]
Therefore, the ILAC G8 and ILAC P14 definition of the TUR denominator closely aligns with the ANSI/NCSL Z540.3 Handbook.
The TUR Formula
From these definitions, we can further define the denominator with specific components of error, as shown in the formula below.

Figure 2: TUR Formula adapted from the ANSI/NCSL Z540.3 Handbook, ILAC G8, and ILAC P14
Some may contend that resolution is accounted for with repeatability studies. However, if repeatability is equal to zero, then the UUT's resolution must be considered. Therefore, many in the metrology community use this formula because it includes the minimum contributors to calculate TUR correctly.
TUR Calculation Example
Using a real-life example, let's walk through the formula.
Example: Our customer sends us a 10,000 lbf load cell with an accuracy specification of ± 0.05 % of full scale. We use a Morehouse Universal Calibrating Machine to perform the calibration. When 10,000 lbf is applied, the unit reads 10,001 lbf. The display reads by 1 lbf.
Step 1: Calculate the Numerator

Figure 3: TUR Formula Numerator
The device is a 10,000 lbf load cell with an accuracy specification of ± 0.05 %
10,000 * 0.0005 = ± 5 lbf
The upper specification limit is 10,000 + 5 = 10,005
The lower specification limit is 10,000 – 5 = 9,995
Therefore, the Span of the ±Tolerance is 10,005 – 9,995 = 10 lbf

Figure 4: TUR Formula with the Numerator added
Step 2: Calculate the Denominator
For this calculation, reduce everything to 1 standard deviation.
CMC

Figure 5: CMC portion of the denominator
CMC is the uncertainty at the calibrated force. We used a Morehouse Universal Calibrating Machine, which achieved an uncertainty of 0.02 % at 10,000.
The CMC is 10,000 * 0.0002 = 2 lbf
kCMC is 2, which was listed on the calibration provider's certificate.
By dividing the CMC by 2, we reduce to standard uncertainty. In most cases, the CMC uncertainty component is reported at 95 %, and a coverage factor close to 2 is used.

Figure 6: TUR Formula with CMC added
Resolution UUT

Figure 7: Resolution portion of the denominator
ResolutionUUT for force instruments is calculated by dividing the force applied by the output at capacity and then multiplying this by the instrument's readability.
The ResolutionUUT is (10,000 lbf / 10,000 lbf) * 1 = 1 lbf
The 1 lbf resolution is often divided by the square root of 12, two times the square root of 3. Reducing the resolution to a standard uncertainty typically is done via a rectangular distribution (square root of 3) or two times two times the square root of 3. Most distributions are rectangular, and since the resolution on a digital indicator has an equal probability of being between -0.5 lbf and +0.5 lbf, we have no way of knowing what the underlying value is and must assume the value is within ± 0.5 lbf. Thus, we will have an uncertainty of ± half the change represented by what our display reads. To get the standard uncertainty in this scenario, we can either take half the resolution 0.5 and divide by the square root of 3 or divide 1 by the square root of 12.
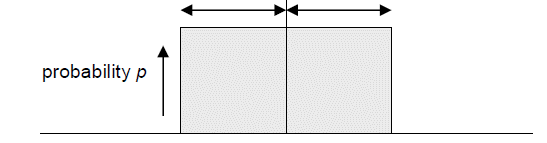
Figure 8: Rectangular distribution of probability
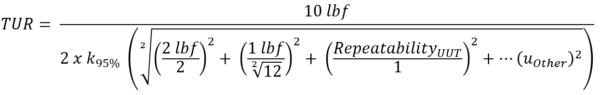
Figure 9: TUR Formula with Resolution added
Repeatability

Figure 10: Repeatability portion of the denominator
Here is where things get a little tricky. How well does the unit repeat in the test scenario? You can remove the repeatability contribution to CMC in the formula and substitute the repeatability of what is being calibrated, but only if the device is similar to the devices used for repeatability used to calculate the CMC. You can decide not to take repeated measurements on the instrument submitted for calibration. For our example, we will take five replicate readings and not recalculate our CMC.
To obtain repeatability, we apply 10,000 lbf to the Unit Under Test (UUT) five times and take the standard deviation of that number.
The Excel formula is STDEV (10,000, 10,001, 10,000, 10,001, 10,001) = 0.54772
The divisor for taking a series of repeated measurements is often considered a normal distribution with a divisor of 1.
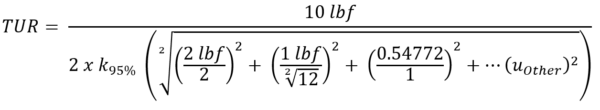
Figure 11: TUR Formula with Repeatability added
Other Error Sources

Figure 12: Other error sources in the denominator
Other error sources can be included for any known error that is not captured in the CMC uncertainty component. Some examples are environmental influences, error in correction factors, etc. For our example, we will assume the Calibration Process Error was calculated correctly and includes the appropriate error sources.
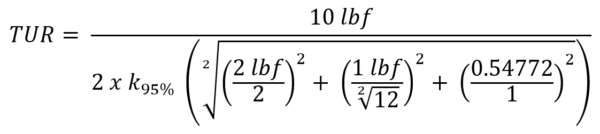
Figure 13: TUR Formula with all error sources added
Reduce the Denominator
If working in Excel, use = SQRT((2/2)^2+(1/3.464)^2+(0.54772/1)^2) = 1.176
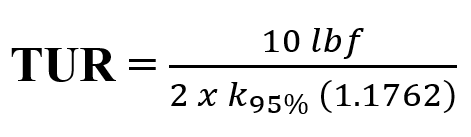
Figure 14: TUR Formula Reduced
We now take our specification of 10 lbf and divide it by the 2 * k at 95 % Calibration Process Uncertainty, which we are using 2 for
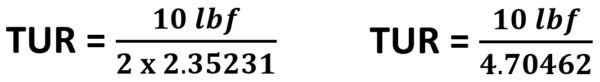
Figure 15: TUR Calculated
TUR = 2.1256
Congratulations, you did it!
By following this example, you can calculate TUR for your calibration. And when you combine this with the measurement location, you can calculate both False Accept and False Reject risk at the time of calibration.
Correctly Calculating TUR Reduces your Measurement Risk
Many of the decision rules found in documents such as the ANSI/NCSL Z540.3 Handbook and ILAC G8 use TUR to help calculate their measurement risk. When TUR is calculated correctly, it helps you reduce measurement risk.
Standards are written with the best intentions, but often they leave too much room for interpretation. When the new ISO/IEC 17025:2017 was released, the standard switched away from conventional norms to take on a risk-based approach. Now more than four years later, we lack agreement on definitions, specifically an understanding of how to calculate TUR and apply the inputs to calculate our agreed-upon decision rule.
When discussing decision rules, we describe how measurement uncertainty is accounted for when stating conformity with a specified requirement. This cartoon explains non-binary conformity, and though part of ILAC G8, many want calibration labs to issue a "pass" or a "fail" and not a conditional pass or conditional fail.

Figure 16: Non-Binary Decision Rules
Since people learn in different ways, Morehouse has created whiteboard videos on TUR and Measurement Risk that further explain these important concepts. To read more about TUR, check out our paper, Why a 4:1 TUR is not enough: The importance of analyzing the probability of false accept risk.
If you find any of this confusing or need further information, do not feel bad. The concepts covered in this blog and the videos are part of a more extensive course that takes several days to complete. Learn more about the Morehouse training programs, which include weeklong digital classes on force measurement errors, focusing on measurement uncertainty. To learn more about force calibration, download our eBook Force Calibration for Technicians and Quality Managers.

References
1. ANSI/NCSLI Z540.3-2006 "Requirements for the Calibration of Measuring and Test Equipment."
2. ILAC G8:2019 "Guidelines on Decision Rules and Statements of Conformity."
3. ANSI/NCSLI Z540.3-2006 "Requirements for the Calibration of Measuring and Test Equipment."
4. ANSI/NCSL Z540.3 Handbook "Handbook for the Application of ANSI/NCSLI 540.3-2006 - Requirements for the Calibration of Measuring and Test Equipment."
5. ILAC G8:2019 "Guidelines on Decision Rules and Statements of Conformity."
6. ILAC P-14:09/2020, "Policy for Uncertainty in Calibration," clause 5.4
7. ILAC P-14:09/2020, "Policy for Uncertainty in Calibration," clause 4.3 note 2
If you enjoyed this article, check out our LinkedIn and YouTube channel for more helpful posts and videos.
#How to Calculate TUR


