Examining the History of TAR and TUR
Why examine TAR and TUR? Hasn’t each topic been covered for decades now?
When we look at TAR and TUR concepts, we find that many in the metrology community have adopted TUR. Both guidance documents and standards have moved away from TAR. However, when we look at the laboratories making measurements, they are decades behind the latest standards and guidance documents.
On many purchase orders, there is still language such as NIST traceable calibration where the standard must be four times more accurate than what is being tested. Essentially, the request is saying we expect that you purchased a standard with manufacturers' specifications or accuracy claims that are at least four times greater than the equipment we are about to send for calibration or know a bit about measurement uncertainty. Maybe we take the ratio of the tolerance and divide that by the measurement uncertainty of our equipment.
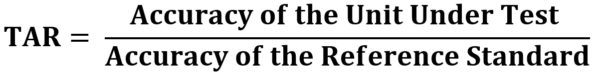
Hence the concept of TAR is simply a ratio comparing the accuracy of the unit under test with the accuracy of the reference standard. Pretty simple, right? Though simplistic, it is riddled with issues because accuracy is not the same as uncertainty, and calculating uncertainty correctly is a requirement of ISO/IEC 17025 and several additional ILAC documents examined later in this blog.
Suppose they do not follow all the guidelines outlined in these documents. In that case, they will likely confuse accuracy with uncertainty and omit many uncertainty contributors that make an instrument look so much better than it is. In these cases, some manufacturers take shortcuts and proceed with a game of accuracy specsmanship.
They may omit significant error sources like reproducibility or resolution, and base specifications on averages rather than good metrological practices. Thus, taking the approach of comparing the accuracy of each instrument against another does not follow well-established metrological guidelines. Not to mention, when TAR is used, and uncertainty is not calculated correctly, which is likely the case when accuracy is substituted for uncertainty, your measurements are not traceable!
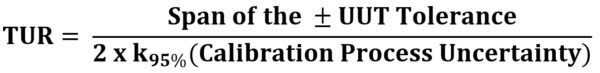
TUR compares the Span of the ± UUT Tolerance and divides that by twice the Calibration Process Uncertainty (CPU). This describes the actual capability of the calibration lab by defining the calibration process uncertainty.
If followed correctly, the definition of TUR gives the end-user a meaningful ratio. The ratio can be used to calculate the risk associated with the equipment calibration. That calculated risk can then be used in a meaningful way to make decisions.
Is the medical equipment used for my surgery tested properly? Are parts of the airplane I'm flying on tested so it doesn't break up in mid-flight? Is the high rise I live in or the hotel I'm at appropriately built so it does not collapse?
If the testing is conducted with equipment based on accuracy specifications alone, there can be significant problems, and your safety is likely impacted. To further understand TAR and TUR, we need to know how TAR came into existence.
History of Measurement Decision Risk Related to TAR and TUR
The roots of measurement decision risk can be traced back to early work done by Alan Eagle, Frank Grubbs, and Helen Coon, which include papers published around 1950. These measurement decision risks concepts were complex for many and did not gain much traction.
About five years later, Jerry Hayes of the United States Navy established accuracy ratios versus decision risks for the calibration program. TAR was introduced because it simplified much of the measurement decision risk. First, a consumer risk of 1 % was accepted, which would be a Probability of False Accept (PFA) today. This means that about a 3:1 accuracy ratio would be required.
Then, working with Stan Crandon, Hayes decided to add this ratio to account for some uncertainty in the reliability of tolerances. Thus, 3:1 became 4:1, and the US Navy adopted a policy that was also adopted by many in the metrological community. More details about this history are found in "Measurement Decision Risk – The Importance of Definitions" by Scott Mimbs.¹
Since there was limited computing power, the 4:1 TAR ratio was an easy-to-follow rule that solved a problem. The TAR is a ratio of the tolerance of the item being calibrated divided by the accuracy of the calibration standard. Thus, if I have a device that needs to be accurate to 1 %, then I need a calibration standard that is four times better, or 0.25 %. Since the concept was so simple, many followed it and continued to follow it. Initially, TAR was supposed to be a placeholder until more computing power became available to the masses.
In the 1990s, we had enough computing power, and TUR should have replaced the TAR concept. More computing power did become available, and it is rumored that ANSI/NCSL Z540-1-1994 originally contained TUR, and at the last minute, edits were made to change TUR back to TAR. When we look at these concepts, we can question why it took five decades to replace TAR with TUR.
TUR is not simple enough for masses and relies on arguably more complex calculations than TAR. Therefore, it is elementary to understand why many still opt to keep using TAR. Let us look at TUR in a bit more detail.
TUR is a ratio of the tolerance of the item being calibrated divided by the uncertainty of the entire calibration process. Evaluation of the TUR is a rigorous process that includes additional contributors to the uncertainty beyond just the uncertainty of the calibration standard. ANSI/NCSLI Z540.3 and the Handbook published in 2006 have the complete definition of TUR. It relies on knowing how to calculate uncertainty following a calibration hierarchy, including metrological traceability.
Today, there are still laboratories using TAR, TUR, and Test Value Uncertainty (TVU). No matter what acronym you use, it is essential to understand the potential shortcomings of using outdated terms. In 2007 Mr. Hayes reflected on his earlier work, “the idea was supposed to be temporary until better computing power became available or a better method could be developed.”¹
In 2021 we certainly have more computing power available, and TAR should be RIP ASAP. Remember when they buried the word "DEF"? Maybe we, as metrologists, need to do that with TAR. We will examine it in more detail and let you decide after learning about the difference between TAR and TUR. First, we must understand Metrological Traceability.
Metrological Traceability, Not Traceable to NIST
The International Vocabulary of Metrology (VIM) defines metrological traceability as the "property of a measurement result whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty."²
The International System of Units (SI) is at the top of the measurement hierarchy pyramid (Figure 1). The next tier in the pyramid is a National Metrology Institute (NMI) such as the National Institute of Standards and Technology (NIST), which is recognized by the International Committee for Weights and Measures (CIPM) and has derived its capability from these base SI units of better than 0.0005 %.
Per NIST, "Metrological Traceability [3] requires the establishment of an unbroken chain of calibrations to specified reference standards: typically national or international standards, in particular realizations of the measurement units of the International System of Units (SI). NIST assures the traceability to the SI..."³ Therefore, traceability is not to NIST. Calibration is performed using measurement standards traceable to the SI through a National Metrology Institute (NMI), such as NIST.
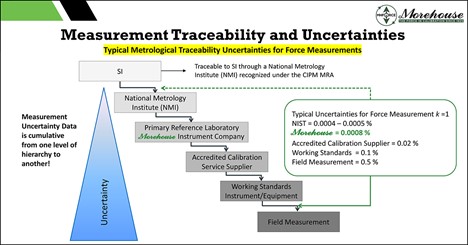
Figure 1: Metrological Traceability Pyramid for Force Measurements
Why is Measurement Uncertainty Important?
If you are accredited to ISO/IEC 17025:2017, the uncertainty of the measurement is required to be reported on a certificate of calibration. This is essential because your customer may want you to make a statement of conformance on whether the device or artifact is in tolerance or not. Additionally, if you do a test and want to know if the device passes or fails, then it may be a consideration.
Measurement Uncertainty is required to establish your measurement traceability. It is crucial because you want to know that the laboratory performing the calibration of your device or artifact can perform the calibration. If you need a device to be known to be within less than 0.02 %, then you must use a calibration provider that gives you the best chance of achieving that result. If the calibration provider has a stated measurement uncertainty of 0.04 %, then mathematically, they are not the right calibration lab to calibrate or verify your device or artifact.
Measurement uncertainty also keeps us honest. If a laboratory claims Traceability to SI through NIST, then the larger the uncertainty becomes, the further away it is from NIST. Figure 1 shows that the further away from SI units, the more significant the uncertainty. For example, field measurement is six steps away from SI. Measurement uncertainties get larger at each level and end at a standard uncertainty of 0.5 %. If we try to build this pyramid using TAR, what happens? Can it work?
We will examine these questions in our next blog, TAR versus TUR: Why TAR should be RIP ASAP. It will cover when TAR works and when it doesn’t work and how TUR is a less risky approach to risk mitigation.
To learn more, watch our video on Understanding Test Uncertainty Ratio (TUR).
If you enjoyed this article, check out our LinkedIn and YouTube channel for more helpful posts and videos.
- Measurement Decision Risk – The Importance of Definitions, Scott Mimbs https://ncsli.org/store/viewproduct.aspx?id=16892913
- Vocabulary of Metrology (VIM)
- NIST Policy on Metrological Traceability



