Device Resolution and the Impact on Consumer Risk - Intro
If a device's uncertainty has too coarse of a resolution, then you need a device that does not subject the conformance decision to higher risk. This blog will present examples that demonstrate why best practices should be followed for conformity assessments rather than drafting individual test protocols and standards.
Best practices are outlined in guidance documents, policy documents, and standards documents such as ANSI/NCSLI Z540.3, ILAC-P14, and ISO/IEC 17025:2017. This is part of an ethical approach to calibration that avoids shifting more risk to the Industry and ultimately mitigates global consumer risk.
Definition and Calculation of Test Uncertainty Ratio (TUR)
Understanding Test Uncertainty Ratio (TUR) is the first step in weighing the significance of the claims proposed in this blog. TUR is defined as:
- The ratio of the span of the tolerance of a measurement quantity subject to calibration to twice the 95% expanded uncertainty of the measurement process used for calibration. [1]
- The ratio of the tolerance, TL, of a measurement quantity, divided by the 95% expanded measurement uncertainty of the measurement process where TUR = TL/U. [2]
These definitions are similar, but the span of the tolerance in the numerator must be clearer. If the tolerance is not symmetrical, then ANSI/NCSL Z540.3 is much clearer.
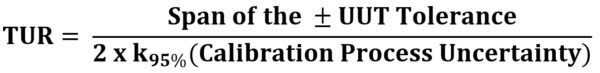
Figure 1: TUR Formula found in ANSI/NCSLI Z540.3 Handbook
The calculation of TUR is crucial because it is a commonly accepted practice in making a statement of conformity. When used in combination with the measurement location, one can calculate measurement risk at the time of calibration. TUR is clearly defined in standards such as ANSI/NCSL Z540.3 and the ANSI/NCSL Z540.3 Handbook. However, equipment manufacturers participate in the practice of writing unique standards that favorably market their products. In reality, the products' application may vary, and acceptance requirements may change depending on the application. Therefore, the failure to adhere to clearly defined, universal standards can put customers or consumers at increased risk.
Accreditation bodies' recommended requirements on the contributors to Measurement Uncertainty should be considered by the end user to aid in calculating the optimal TUR. One may argue that the reference standard uncertainty and environmental factors are the only requirements needed in the TUR calculation to make a conformity assessment decision. Make no mistake: TUR is defined and agreed upon in ANSI/NCSL Z540.3:2006 and the ANSI/NCSL Z540.3 Handbook. Therefore, it should not be a point of debate.
The definition of CPU establishes whether relevant uncertainty contributors of the customer's device will be considered by the calibration laboratory that is calibrating the equipment. If a calibration laboratory does not include these uncertainty contributors, then they are passing the risk on to the customer or consumer because the laboratory prefers not to retain the risk. This is often done without the end user's knowledge.
Evaluating Global Consumer Risk
The customer or consumer is likely a company making a measurement that could have an impact on public safety. Henry Petroski addresses this issue in his book To Engineer is Human: The Role of Failure in Successful Design: "Failures appear to be inevitable in the wake of prolonged success, which encourages lower margins of safety. Engineers and the companies who employ them tend to get complacent when things are good; they worry less and may not take the right preventative actions."[3] Petroski's statement about complacency may describe what is happening in the metrology community today regarding the evaluation of global consumer risk.
Global consumer risk is defined in JCGM 106:2012. The role of CPU in conformity assessment is defined as "the probability that a non-conforming item will be accepted based on a future measurement result." [4]
When laboratories loosen the restraints or fail to capture the proper contributors while calculating CPU to make a statement of conformity, they are creating a risk wherever this equipment will be used. The application could be weighing an aircraft or overhead material handling, where lives are at stake.
How Calibration Chain Hierarchy Impacts Risk Propagation
If only one tier of the calibration chain cares about the measurement decision risk, then the whole process is at risk. When this risk is propagated throughout succeeding tiers, can we expect the process to work properly?
Metrological traceability is defined as the "property of a measurement result whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty."[5] The International System of Units (SI) is at the top of the measurement hierarchy pyramid.

Figure 2: Metrological Traceability Pyramid for Force Measurement
The next tier in the pyramid is a National Metrology Institute (NMI), such as the National Institute of Standards and Technology (NIST) and other designated institutes recognized under the CIPM MRA. In the example above, the third tier is a commercial laboratory, such as Morehouse Instrument Company, with primary standards for force and torque. The lower tiers are accredited calibration suppliers, followed by working standards, with field measurement at the bottom.
In an ideal world, each of these tiers should use the same methods to calculate CPU. Suppose any tier in this pyramid uses a different formula for CPU or neglects critical contributors to the measurement uncertainty. In that case, the next tier will under-report the measurement uncertainty, thereby increasing the overall risk of product failures (PFA – Probability of False Accept).
Considerations for Evaluating Measurement Uncertainty
To meet the metrological traceability requirements, measurement uncertainty must be properly evaluated, taking into consideration the minimum number of contributors. Measurement uncertainty is defined as a "non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand, based on the information used."[5]
In simplistic terms, measurement uncertainty may be thought of as doubt or, in effect, doubting the validity of the measurement. CPU is the non-bias uncertainty ascribed to the result of a measurement at a particular test point. It is crucial for calculating the Test Uncertainty Ratio (TUR), as shown in Figure 1.
Most likely, a general industry manufacturer will not calculate the measurement uncertainty associated with their measuring equipment. Although they bear some responsibility, they may not understand their equipment or how to calculate measurement uncertainty. The metrology community has spent decades putting proper measurement uncertainty practices in place. However, the general industry manufacturer is lagging decades behind these practices.
For example, many general industry manufacturers are still using outdated concepts, such as Test Accuracy Ratio (TAR) and NIST traceability. The metrology community has moved away from these terms, but both are still implemented instead of sound metrological practice.
Metrological traceability relies on tracing the measurement chain back to SI units. The proper way to claim metrological traceability is to trace each calibration back to the SI through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty. The chain will often end with an NMI such as NIST, which is recognized under the CIPM MRA. Assuming that the end-user will understand the risk seems like a rationalization for equipment manufacturers to sell more products and increase profit margins while knowing full well that the burden of risk is thrust upon the end user.
Many do not agree on which contributors should be included in a measurement uncertainty evaluation. Some argue that the UUT's resolution does not need to be included in an uncertainty evaluation. However, if the uncertainty evaluation does not consider known contributors to measurement uncertainty, there is a question of whether the calibration can even be metrologically traceable or accredited.
In such a scenario, a calibration laboratory cannot make a statement of conformity or "Pass" an instrument without violating ISO/IEC 17025:2017, which states, "When a statement of conformity to a specification or standard is provided, the laboratory shall document the decision rule employed, taking into account the level of risk (such as false accept and false reject and statistical assumptions) associated with the decision rule employed, and apply the decision rule."[6]
The United Kingdom Accreditation Service (UKAS) elaborates on this point: "Conformity statements under ISO/IEC 17025:2017 require a Decision Rule (3.7) that takes account of measurement uncertainty. Some people argue that it is possible to 'take account' by ignoring it if that is what the customer requests; however, this seems to require a rather contradictory belief that you can be 'doing something' by 'not doing something' (is it possible to 'obey a red stoplight' by 'not obeying a red stoplight'?)." [7]
The UUT resolution is a relevant short-term contributor for consideration in the measurement process uncertainty to the customer's device, and it should not be ignored.
Example #1: Comparing Resolution for a Dimensional Measurement
Think about a user making a measurement with a caliper and a micrometer with different resolutions. In Figure 3, someone is using a caliper to make a measurement. The drawing specification is ±0.000 5 in., and the user has a caliper and wants to know if the part is within tolerance.

Figure 3: User measuring a part with a caliper with a resolution of 0.000 5 in.
Suppose the laboratory that calibrated the caliper ignored measurement uncertainty contributors, such as the device's resolution and repeatability. Would the user know to shrink the acceptance limit on the drawing so they can say with little doubt that the part is in tolerance? Is the device with a resolution of 0.000 5 in. good enough for the operator to call the part in tolerance? Would the experienced operator instead choose a micrometer to measure the part? The answer to all three of these questions is the same: not necessarily.
In Figure 4, the same item is measured with a micrometer that is capable of reading 0.000 1 in. In one instance, the reading is 0.308 0 in., and in another, the reading 0.308 3 in.

Figure 4: User measuring a part with a micrometer with a resolution of 0.000 1 in.
Example #2: Comparing Resolution for a Weight Measurement
Consider a crane scale that is used to measure the weight of an object. Suppose the laboratory that calibrated the crane scale based the decision rule only on the calibration equipment and not on the crane scale's repeatability or resolution. Would the crane scale operator know to guard band the tolerance at the point of use?
The user has a scale that is known to read with a resolution of 0.1 kg. They need to measure 1 000 kg of uranium to within ± 0.1 kg. Will they guard band to keep what they are weighing within 0.07 kg? Figure 5 illustrates how the user would guard band by subtracting the measurement uncertainty.

Figure 5: Guard band and acceptance interval illustration found in ILAC G8:09/2019
Will you feel confident that measurements were performed correctly and, when applied, will keep you safe—or will you worry about your safety? How do you feel now knowing that someone may have failed to calculate and apply measurement decision risk correctly? Having to question if the people making the measurements may have understated the calibration measurement process uncertainty does not boost confidence.
Device Resolution and the Impact on Consumer Risk - Outro
We will examine these questions in our next blog, The New Dimension to Resolution: Can it be Resolved? It will cover how manufacturers and calibration laboratories should correctly calculate both uncertainty and risk on equipment.
To learn more, watch our video Minimize your Force and Torque Measurement Risk.
References
1. ANSI/NCSLI Z540.3-2006 "Requirements for the Calibration of Measuring and Test Equipment."
2. ILAC G8:2019 "Guidelines on Decision Rules and Statements of Conformity."
3. To Engineer is Human: The Role of Failure in Successful Design, by Henry Petroski
4. JCGM 106:2012_E clause 3.3.15 "Evaluation of measurement data – The role of measurement uncertainty in conformity assessment."
5. JCGM 200:2012 International Vocabulary of Metrology (VIM)
6. ISO/IEC 17025:2017 "General requirements for the competence of testing and calibration laboratories," clause 7.8.6.1
7. UKAS LAB 48 Decision Rules and Statements of Conformity
If you enjoyed this article, check out our LinkedIn and YouTube channel for more helpful posts and videos.



