Delving into Specific Risk: A Comprehensive Understanding of PFA and PFR
Specific risk in metrology, mainly focusing on the Probability of False Acceptance (PFA) and Probability of False Rejection (PFR).
These concepts are crucial in the decision-making process based on measurement results.
Specific Risk
Specific risk, as the term suggests, is a risk that is specific to a given test measurement result.
It is often thought of as controlling the quality of individual workpieces or examining the individual measured values on the test, measuring, and diagnostic equipment (TMDE).
It is the probability that a test measurement result indicates a product is within specifications when it is actually outside specifications.
This risk arises due to the inherent uncertainty in the test measurement.
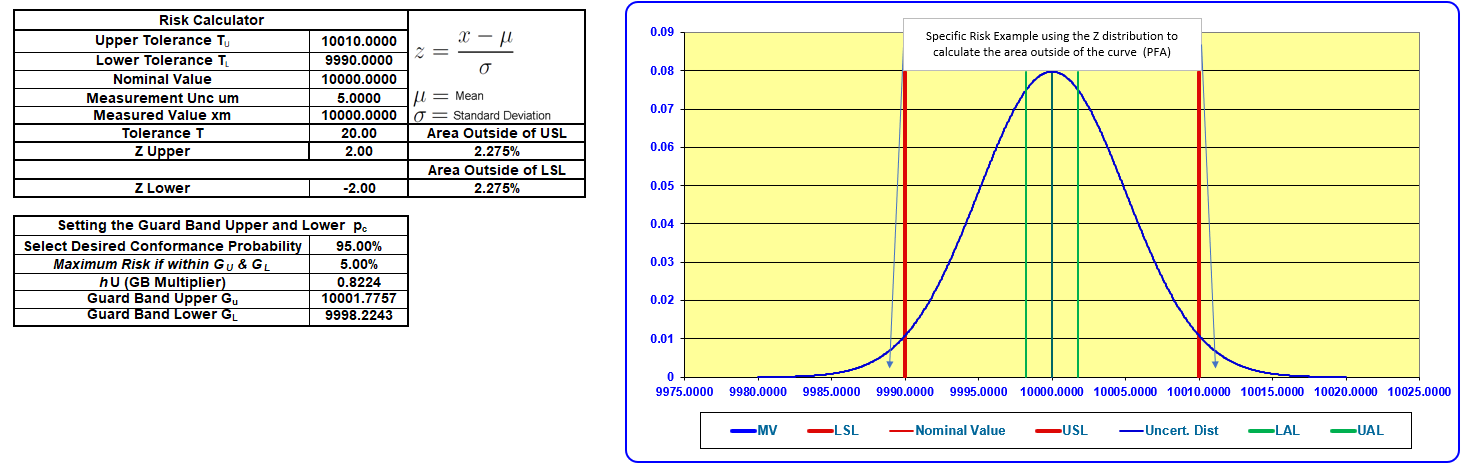
To visualize this, consider the test measurement uncertainty's Probability Density Function (PDF).
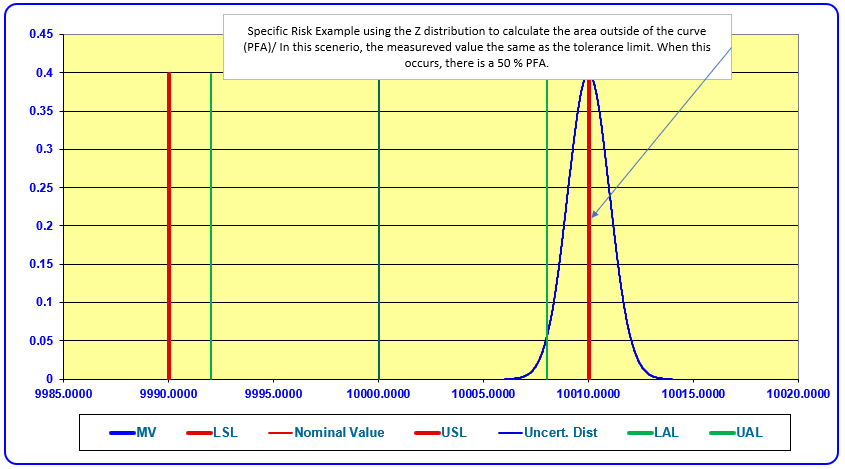
The specific risk is illustrated where the upper tail of the probability curve falls above the upper specification limit and the lower tail of the probability curve falls below the lower specification limit.
The area under this curve represents the probability (specific risk) of incorrectly accepting a product given this measurement result.
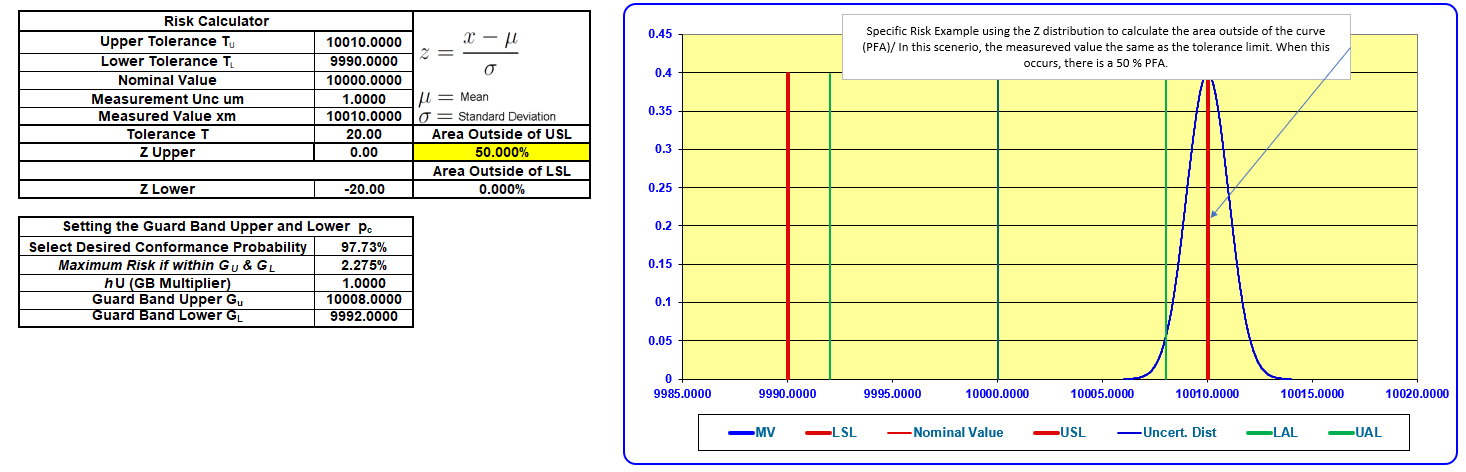
The above example uses an extreme scenario where the expanded measurement uncertainty equals the tolerance limit.
The guard band multiplier is calculated for the desired conformance probability. In this case, that is 95 %.
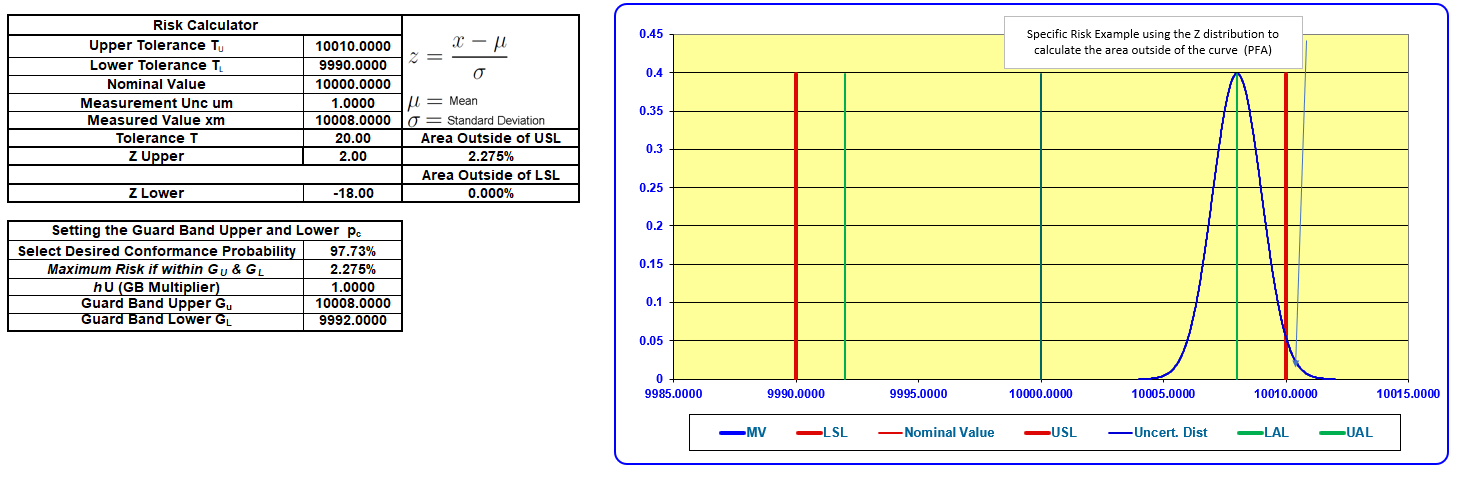
In our second example above, we have changed the 95 % Expanded Measurement Uncertainty; this time, we have a 5:1 ratio. We changed the desired performance probability to 97.73 %, limiting our risk to 2.275 % recommendation from ANSI Z540.3 and other documents.
This might throw some people for a loop, meaning they thought the recommendation was 2 %.
Well, it is, though all the calculations were based on a coverage factor equaling 95.45 %, and when we subtract 95.45 % from 100 %, we get 4.55 %.
If we take half of that, we get 2.275 %. Now, back to our examples.
When we change the measurement location to the exact location our GB Multiplier indicates, we can record the measured value and have the risk (probability of non-conformance) equal 2.275 %.
Some might be saying, What is a guardband multiplier?
Several examples in ILAC G8, JCGM 106, UKAS LAB 48, ISO 14253-5, and ASME B89.7.4.1 explain Guard band multipliers.
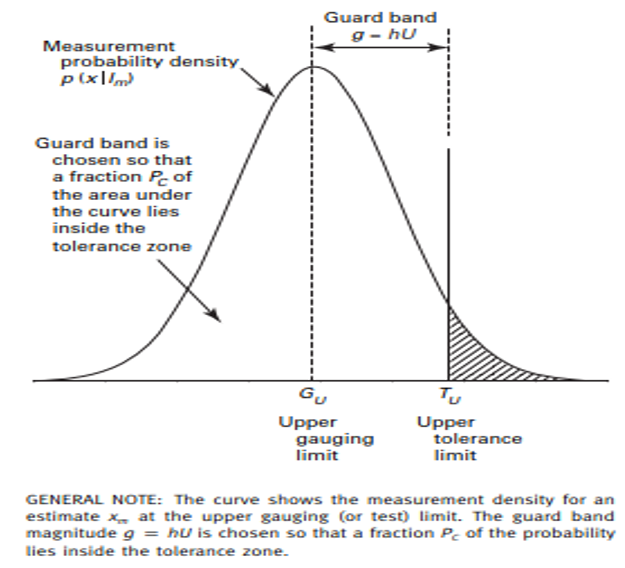
The simplest explanation comes from ASME B89.7.4.1, which discusses a guard band multiplier being set to assure conformance probability.
The guard band is chosen to set the maximum limit to achieve a desired conformance probability.
When the measured value is at the upper acceptance limit (the upper gauging limit above), the area outside the curve will equal the desired maximum risk.
While the rest of the curve inside of the Tolerance Limit will be the probability of conformance to the specification.
What happens when we do not use guard bands to limit risk?
Several in the industry, not Morehouse by any means, often take a "shared risk" approach. We choose by default to limit the PFA to less than 2.275 % per method 5 of the ANSI/NCSL Z540.3 handbook.
What "shared risk" means is as long as the measured value is less than or equal to the tolerance, the value is reported, and it is agreed upon that this is okay.
You may not be okay with it, though many are not applying guard bands and taking the approach that the end-user can decide if it's good or bad.
ISO/IEC 17025:2017 dictates that the customer must agree upon the decision rule when a statement of conformity is to be made.
The customer shall specify the tolerance requirements for conformity. If no conformance requirement is requested, then the decision rules requirement is unnecessary.
Simply put, regarding decision rules, if you choose not to decide, you still have made a choice (Shared Risk).
Under this scenario, the consumer can bear as much as 50 % of the measurement risk. If the UUT propagates measurement uncertainty further, a PFA higher than 50 % is more likely to occur.
However, the test and calibration provider must still report the measurement result and its associated measurement uncertainty.
Thus, as a customer, you could have a much higher level of risk than you wanted.
PFA and PFR as they Relate to Specific Risk
Now, let's delve into the concepts of conditional PFA and PFR.

The Probability of False Acceptance (PFA), also known as consumer risk, Type II error, is the probability that a test measurement on any product results in an incorrect pass determination.
On the other hand, the Probability of False Rejection (PFR), also known as producer's risk, Type 1 error, is the probability that a measurement result indicates a product is outside the limits when its actual value is actually within the limits.
Both PFA and PFR are integral to understanding and managing specific risk.
They provide a quantitative measure of the risk associated with a particular measurement result, guiding the decision-making process.
For instance, a high PFA indicates a high risk of incorrectly accepting a product that is out of specification.
This could lead to potential issues, such as product failures or customer dissatisfaction.
On the other hand, a high PFR indicates a high risk of incorrectly rejecting a product that is actually within specification.
In the case of shared risk, when the measured value is equal to the tolerance, the Specific (FR Risk) PFR is also 50 %.
This could lead to unnecessary costs and wastage for the producer.
By understanding and managing PFA and PFR, laboratories and their personnel can make more informed decisions about accepting or rejecting equipment based on the measurement result.
This can significantly improve the reliability and accuracy of measurement results, thereby enhancing the overall quality of measuring equipment and services.
Moreover, understanding PFA and PFR can also help in defining the decision rules to be applied by laboratories.
These decision rules are directly in the control of recipients of statements of conformity as they specify the decision rules to apply.
Therefore, the recipient takes the specific risk associated with statements, that is, false acceptance or rejection of results.
Specific Risk Conclusion
In conclusion, conditional specific risk, PFA (Conformity to the specification), and PFR (non-conformity to the specification) are critical concepts in metrology that help make informed decisions based on measurement results.
Understanding and managing these risks can significantly improve the reliability and accuracy of measurement results, thereby enhancing the overall quality of products and services.
As we continue to advance technologically, the role of these concepts in enhancing productivity and efficiency will only become more significant.
Furthermore, any decision rule describes how measurement uncertainty is accounted for when stating conformity with a specified requirement.

The figure above shows a specific risk scenario with a larger acceptance interval when the measurement uncertainty is low and a smaller acceptance interval when the measurement uncertainty is high.
Morehouse uses primary standard deadweight calibrations up to 120,000 lbf for force measurements, ensuring measurement uncertainties are kept low, allowing us to use more comprehensive acceptance limits and "pass" more equipment sent to us for force calibration.
If you enjoyed this content on specific and global risk, check out our LinkedIn and YouTube channel for more helpful posts and videos.
Everything we do, we believe in changing how people think about force and torque calibration.
We challenge the "just calibrate it" mentality by educating our customers on what matters educating them on specific risk so that anyone can apply the appropriate guard banding strategy.
Morehouse makes simple-to-use calibration products.
We build fantastic force equipment that is plumb, level, square, and rigid and provide unparalleled calibration service with less than two-week lead times.
Contact us at 717-843-0081 to speak to a live person or email for more information.
# Specific Risk
Specific Risk References
- ASME B89.7.3.1-2001Guidelines for Decision Rules: Considering Measurement Uncertainty in Determining Conformance to Specifications
- ASME B89.7.4.1-2005 Measurement Uncertainty and Conformance Testing: Risk Analysis
- JCGM 106:2012 Evaluation of measurement data – The role of measurement uncertainty in conformity assessment
- ILAC G8:09/2019 Guidelines on Decision Rules and Statements of Conformity
- ISO 14253-5 Part 1: Decision rules for proving conformity or nonconformity with specifications
Check out another article on Specific versus Global Risk here.


