TAR versus TUR: Why TAR should RIP ASAP
In our last blog, Examining the History of TAR and TUR, we examined several outdated, and to some extent wrong, practices, such as Test Accuracy Ratios (TARs) and requesting NIST traceable calibrations. Remember when they buried the word "DEF"? Maybe we, as metrologists, need to do that with TAR. We will examine it in more detail and let you decide.

TAR – When it Doesn't Work
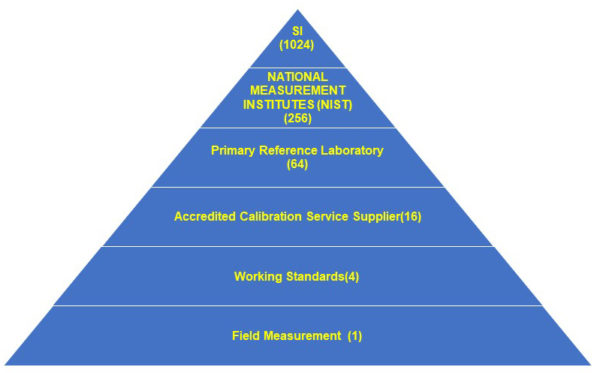
Figure 1: Test Accuracy Ratio (4:1)
When using a 6 step pyramid to figure out TAR, it is not sustainable if it needs to be four times better at every step. The working standards could be four times better than the field measurement. The accredited calibration provider might be sixteen times better than the process measurement. However, by the time we get to the primary reference laboratory, NIST, and SI, we cannot maintain the 4:1 ratio.
This example gets complicated when the different tiers claim lower-than-expected uncertainties. For instance, some working standards laboratories are accredited at numbers unbelievably low, such as 0.05 %. The accredited calibration service supplier cannot be four times better at 0.02 %. In today's world, many uncertainties are under-reported, and a 4:1 ratio is not maintainable.
When technology was in its infancy, TARs were easy. However, the early system typically had very conservative specifications, and the expectation was not to the tightest tolerances achievable. As a result, technology sometimes eclipsed the standards and requirements. One example is a National Bureau of Standards Certificate for Thomas 1 Ohm with an uncertainty of ± 1.5 ppm. Now that exact measurement is readily achievable on a Fluke 8508.
I caution others to watch out for TAR numbers like 4:1 or 10:1, because they may later find out the real uncertainty is high or that uncertainty is under-reported. This highlights one of the main problems with TARs, which is that they are not generally accepted standards, such as ASTM & OIML.
A great example is The Quest Metrology Thread measuring system, which was "accurate" to ±1µin. However, the uncertainty was ±30µin because the best calibration system was only able to achieve ±30µin. In practice, it certainly seemed capable of resolving and repeating a much lower number. The lesson for us is to know and understand Metrological Traceability and apply the fundamentals to our measurement uncertainty calculations.
TAR – When it Works
TAR can work with procedures that have clear guidance and when the end-user can control the systems they use. We can use a small ratio and pretty easily maintain a TAR. One of the best examples where this works is the ASTM E74 standard.
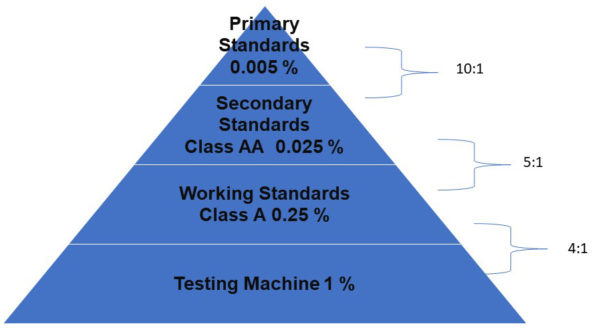
Figure 2: ASTM E74 Ratios
ASTM E74 was developed in 1974 and has a statistical approach that randomizes the condition of the measurement, capturing the reproducibility condition well. The standard uses 30 or more data points and uses these to generate a pooled standard deviation. The agreed-upon formulas are such that about 98 % of the error is captured at calibration time.
The caveat is that the end-user is still responsible for doing additional testing using their machines and understanding that changing adapters, loading conditions, and the environment will increase the error. In general, with the agreed-upon formula, the ratios in Figure 2, work well.
When the ASTM standard is combined with a robust Proficiency Test Plan, Statistical Process Control, and the additional accreditation guidelines for measurement uncertainty, the standard is the defacto method to ensure your force-measuring system is as good as needed. If you want to mitigate measurement risk, calculate measurement uncertainty correctly, and make better measurements, strongly consider having your force-measuring equipment calibrated to the ASTM E74 standard.
This example shows how TAR can work well in a controlled environment. That environment may be the end-user specifying their equipment for use and the appropriate equipment or laboratory for calibration. When you specify the exact equipment, you can do internal testing and make the appropriate determinations for your needs.
When you know that only two to three measurement tiers will be used, you can choose the measurement process and equipment based on a large sample with actual testing to maintain a four-to-one requirement. At the least, you can run the tests and make the determination. Typically, this requires a lot of tests and knowledge. In contrast, if you do not know the system, there is a much stronger case for Test Uncertainty Ratios using the appropriate method and guardband for their application.
TUR Defined
Many in the metrology community have invalidated TAR because it does not align with metrological traceability practices. They prefer TUR because uncertainty is cumulative from one level of the hierarchy to another. They argue that it carries a much less risky approach to risk mitigation. To understand how it works, we must define TUR.
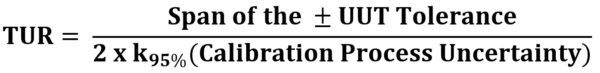
ILAC PP14:09/2020 and the ANSI/NCSLI Z540.3 Handbook are two that reference and define TUR. TUR is defined as:
- The ratio of the span of the tolerance of a measurement quantity subject to calibration to twice the 95% expanded uncertainty of the measurement process used for calibration.1
- The ratio of the tolerance, TL, of a measurement quantity divided by the 95% expanded measurement uncertainty of the measurement process where TUR = TL/U.2
These definitions are similar, but the span of the tolerance in the numerator must be more straightforward. If the tolerance is not symmetrical, then ANSI/NCSL Z540.3 is much clearer. The TUR calculation is drastically different from comparing accuracy ratios as we are now dealing with calculating the calibration process uncertainty (CPU).
The formula's ratio includes a numerator and a denominator. ANSI/NCSL describes, "For the numerator, the tolerance used for Unit Under Test (UUT) in the calibration procedure should be used in the calculation of the TUR. This tolerance is to reflect the organization's performance requirements for the Measurement & Test Equipment (M&TE), which are, in turn, derived from the intended application of the M&TE. In many cases, these performance requirements may be those described by the Manufacturer's tolerances and specifications for the M&TE and are therefore included in the numerator."3

In most cases, the numerator is the Unit Under Test Accuracy Tolerance. The denominator is slightly more complicated. Per the ANSI/NCSL Z540.3 Handbook, "For the denominator, the 95 % expanded uncertainty of the measurement process used for calibration following the calibration procedure is to be used to calculate TUR.
The value of this uncertainty estimate should reflect the results that are reasonably expected from the use of the approved procedure to calibrate the M&TE. Therefore, the estimate includes all components of error that influence the calibration measurement results, which would also include the influences of the item being calibrated except for the bias of the M&TE. The calibration process error, therefore, includes temporary and non-correctable influences incurred during the calibration such as repeatability, resolution, error in the measurement source, operator error, error in correction factors, environmental influences, etc."4
TUR versus TAR
Test Accuracy Ratio (TAR) is an outdated calculation that is not sustainable. It is the ratio of the accuracy tolerance of the unit under calibration to the accuracy tolerance of the calibration standard used. It can be used in situations where the end-user has control protocols where they have thoroughly evaluated the systems. TUR, on the other hand, is well-defined in ANSI/NCSLI Z540.3.
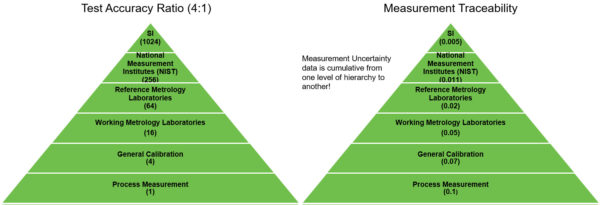
Figure 3: Test Accuracy Ratio vs. Measurement Uncertainties
The measurement uncertainty calculation of TUR is well-defined and always includes the uncertainty contribution of the reference standard used for calibration. Thus, the TUR definition is clear, and when followed it allows for a better conformity assessment. That conformity assessment is key because most end-users want to know if their system passes calibration.
ISO/IEC 17025: 2017 states, "When a statement of conformity to a specification or standard for test or calibration is provided, the laboratory shall document the decision rule employed, taking into account the level of risk (such as false accept and false reject and statistical assumptions) associated with the decision rule employed and apply the decision rule."5 When we combine this statement with the requirements of ILAC P-14 regarding stating measurement uncertainty, we get very good alignment with the definition of TUR.
ILAC P14:09/2020 states, "Contributions to the uncertainty stated on the calibration certificate shall include relevant short-term contributions during calibration and contributions that can reasonably be attributed to the customer's device. Where applicable, the uncertainty shall cover the same contributions to the uncertainty that were included in the evaluation of the CMC uncertainty component, except that uncertainty components evaluated for the best existing device shall be replaced with those of the customer's device. Therefore, reported uncertainties tend to be larger than the uncertainty covered by the CMC."6
Therefore, if we calculate measurement uncertainty correctly per ILAC P-14 and make a conformity assessment, TUR provides a technically well-aligned ratio with accreditation guidelines for calculating Measurement Uncertainty.
Using a calibration provider with low uncertainties will help raise the TUR ratio. The higher TUR will result in broader acceptance (compliance) limits. Wider acceptance limits give more room to account for the bias increase that will occur between calibrations. Therefore, it is essential to consider all sources of uncertainty when determining the time between calibration and tolerance limits. The concept of TUR allows us to make more informed decisions on the equipment we are using for testing. It does not hide significant errors as TAR does as TUR is well-defined. These decisions are often based on defining the appropriate level of risk.
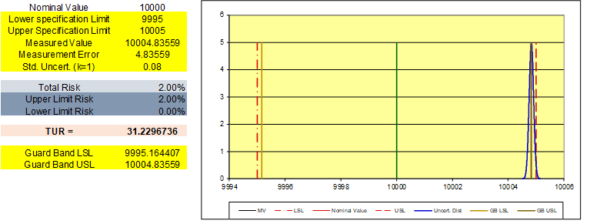
Figure 4: Guard band USL showing a 2 % PFA when Measured Value is at the GB USL
Measurement Risk
All measurements have a percentage of likelihood that they will designate that something is good when it is bad, or something is bad when it is good. This impacts consumer risk, which is the possibility of a problem occurring in a consumer-oriented product. Occasionally, a product that does not meet quality standards passes undetected through a manufacturer's quality control system and enters the consumer market.
The Probability of False Accept (PFA) is similar to the consumer risk. It is the likelihood of calling a measurement "good" or stating something is "In Tolerance" when there is a percentage of chance that the measurement is "bad" or "Out of Tolerance."
With TUR, there are several published methods to calculate measurement risk appropriately. These decision rules rely on a correct calculation of TUR for the conformity assessment. When used correctly, these risk-based approaches help keep the roads we drive on, the planes we fly in, the structures we sleep in, and the everyday items we use from failing at high rates. Good metrological practices simply keep us a bit safer!
Why TAR should RIP ASAP
The metrology community must recognize mandatory policy documents such as ILAC-P14 and guidance documents such as the ANSI/NCSLI Z540.3 Handbook. These documents correctly define the calibration process measurement uncertainty used for calibration. The uncertainty reporting in ILAC P-14 aligns quite well with the definition of TUR in ANSI/NCSLI Z540.3 Handbook. Using the proper definition of TUR is a starting point to use one of the several guard banding methods in ANSI/NCSLI Z540.3, which correctly references calculating TUR.
This blog has presented a lot of information to demonstrate that TAR is outdated and can only work in particular applications. TAR should RIP ASAP for most applications. TUR should be used to make conformity assessments and create a sustainable chain of traceability where measurement uncertainty is correctly accounted for at each tier.
To learn more, watch our video on Understanding Test Uncertainty Ratio (TUR).
- ILAC P14:09/2020
- ANSI/NCSLI Z540.3 Handbook
- ANSI/NCSL
- ANSI/NCSL Z540.3 Handbook
- ISO/IEC 17025
- ILAC P14:09/2020
If you enjoyed this article, check out our LinkedIn and YouTube channels for more helpful posts and videos.
#TAR
#TUR
#TAR versus TUR



